PaleoBabble readers know that ancient astronaut theorists suffer from a fixation on megalithic construction. The “impossibility” of moving stones of great size and tremendous weight appears to them as proof of alien assistance. This argument of course is simply reduced to “since I can’t figure out how it was done, it must have been aliens.” Rather than focus on the absurdity of this logic, I’ve tried to introduce readers to peer-reviewed scholarship on ancient construction and engineering. Egypt’s pyramids have received a lot of attention here in that regard. I want to turn now to Baalbek, specifically the famous trilithon (the three stones at the base of the Roman temple at the site).

There isn’t much written on this that’s available to the non-specialist, and most of what is available isn’t in English. At the risk of directing readers to a source that won’t be much use since it’s in French, I still think it’s useful to demonstrate that scholars have put serious thought into the trilithon, and have come up with workable solutions that have been successful in analogous situations (in this case, something even bigger than the trilithon – yes, ancient alien enthusiasts, the trilithon is NOT the largest object moved without modern machines; keep reading). A very good (and lengthy) scholarly journal article in French about moving the trilithon by ancient mechanical means is available on the web: Jean-Pierre Adam, “A propos du trilithon de Baalbek. Le transport et la mise en oeuvre des megaliths,” Syria 54:1-2 (1977): 31-63 (English translation: “Concerning the trilithon of Baalbek: Transportation and the Implementation of the Megaliths”). Two caveats on the article: (1) It’s very technical. It’s filled with mathematical discussion since its author is quite familiar with analyzing such problems via applied physics; (2) my French stinks. As such, I converted the article to text and used Google Translate, then went through and smoothed things out. I did not do this for the full article (I have better things to do). However, I have given readers important excerpts of this 32 page article. If you read French, then you can check on the translation and send me updates.
On pages 34-37 the author discusses ancient writers who described construction techniques for moving large stone objects. He writes:
“The advantage of this unique publication is exacerbated by the fact that, although written during the reign of Augustus, the treaty made a broad appeal to the art of building Greeks whose author cites the lost works of theorists and the most famous architects. In the context of this brief study, our interest is in the tenth book of Vitruvius, where we find a detailed description of the process and machinery used on construction sites of Greece and Rome and the author mentions at the same time the efficient and widespread job. The transport of megaliths is not forgotten . . .
Vitruvius cites two anecdotes relating to the construction . . . He sank both ends of “column each iron bolts made of Swallow-tailed and are sealed” with lead, having taken the precaution to put in the pieces of wood cross-sectional “dirty iron rings, in which bolts came in as “hubs. In addition, he strengthens his machine by attaching the two “pieces of oak ties, so that when the horse pulling the” bolts turned so easily into the rings, all the “shafts of the columns rolled easily on land to their destination.”
The second transport means for the megaliths described by Vitruvius . . . consisted of wheels twelve feet (approx. 3.60 m) and “locked both ends of the architraves in the middle of the wheels. He put “as bolts and iron rings, so that when the horse” pulling the machine, put the bolts in the iron rings were “turning the wheels. Thus, the architraves, which were in the wheels “as axles, were dragged and taken on the spot.”
He provides the following drawing to illustrate these techniques (Fig 2). Note how the absence of a round shape was no obstacle to moving something like a whole large pillar or obelisk — you simply gave it roundness at the ends to roll it. Very clever.
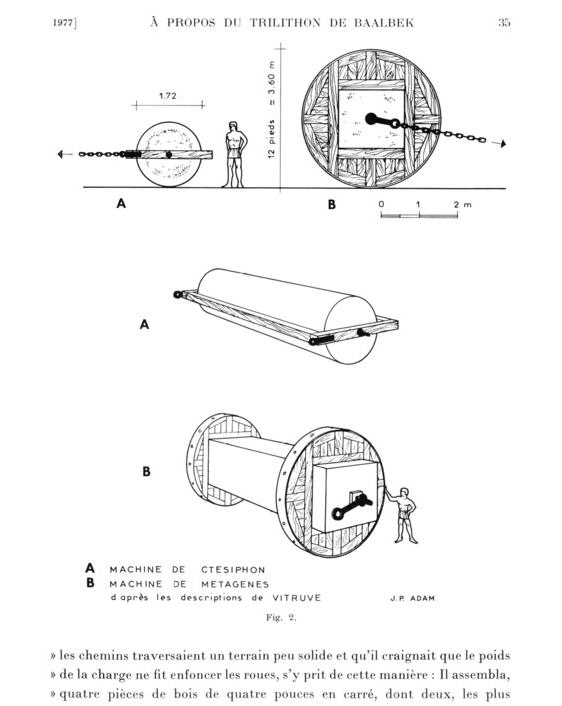
On page 42 the author introduces what will become for him an analogous point of reference for his proposed solution to moving the trilithon of Baalbek:
“. . . 1,250,000 kilograms . . . is the weight of the great block of granite the Empress Catherine II of Russia (1762-1796) . . . carried to St. Petersburg (now Leningrad) to serve as a colossal base to the equestrian statue of Peter the Great. This is likely the largest stone ever moved by man, one and a half times the weight trilithon blocks [at Baalbek.]”
Hope you caught that — an object 1.5 times the weight of the trilithon was successfully moved in the 18th century — no modern cranes. They did it with manpower, not alien know-how. He mentions other large objects successfully moved by human engineers, but this one gets special attention because it was a larger problem than the trilithon.
The rest of the article is devoted to Baalbek’s trilithon. Throughout pages 52-63, the author discusses the physics and engineering problems and solutions. Some excerpts:
“To appreciate the magnitude of the work, and justify the solution adapted to it, it is necessary to give the figures for to the heavier blocks, namely those of trilithon As its name suggests this set consists of three stones measuring respectively, 19.60 m, 19.30 m and 19.10 m long, 4.34 m high, 3.65 m deep. Their average weight is nearly 800 tons. . . . every stone has nearly 10 m in length for an average weight of 350 tonnes . . . After recalling the experiences of St. Petersburg, Luxor, and Carrara, we can obtain a more lucidly clean solution for this megalithic structure and more particularly to the construction of the trilithon.”
The author discusses using ox power to move the stones, a solution he will reject because of the lack of space on the site for the oxen:
“To solve the problem of Baalbek in the most comprehensive, we will consider the establishment of one of the heaviest blocks, that is to say one of the stones of 800,000 kg constituting the trilithon; the interventions for elements lighter in the deduction will be logical.
So either one of these stones completely detached from the rock and relaxing on logs. The floor beams receiving the convoy has a rolling flat surface to reduce the weight hauled to 66,600 kg. Knowing that an ox can provide a work of 80 kgm per second, continuously for one hour, we deduce there should be 825 of these animals to transport one of trilithon stones on a horizontal floor. Traditionally, it is estimated that an ox can pull a load 1.000 kg placed on a chariot. If we consider the block of 800,000 kg of the trilithon, it follows that 800 oxen are needed to move it.”
The author notes some logistical problems with using oxen before moving to a human solution:
“Certainly the yoke was known to mate the oxen, and in the case normal load, the pole was attached directly to the yoke between two animals, but when it came to transport heavy, each torque cattle was connected to the load by a cable or pole. . . . Xenophon gives us a confirmation on the use of this type coupling in the description he gives us the means employed by Cyrus to ensure the movement of heavy battle rounds . . . Each turn with wheels, was equipped with 8 drawbars which were harnessed eight pairs of oxen pulling front.
Despite the apparent simplicity of this energy source, we prefer to look to the human powered, with which the weakness in muscle is compensated by the extreme technical elaboration of the device multiplier used. In the event of a traction provided by the duration of the capstans, movement is a bit longer, since it multiplies the distance traveled by the load, in favor of the force and must ensure the in place and anchor machinery. The advantage of this method lies in the extremely small number of workers needed and the greater accuracy of the progression, allowing rigorous implementation of blocks the one above and beside the other. . . . Each capstan bar with four men using it would make 24 in total. . . . The force exerted directly by the capstan 24 men and six bar is at 20 kg per man of 480 kg. Taking center force application to 1.70 m from the center of rotation and a radius of drum of 10 cm, this force becomes (by a form winch) 8160 kg. Four cables of hemp, each providing four tons of traction, wind around the drum and by acting on the load through a hoist with two pulleys, generate a power of 16,320 kg of the machine; 13,056 kg reduced power by the coefficient of friction. Six of these machines, involving 144 men and providing traction power of 78,336 kg must allow, with a margin of excess power always useful, the transportation of each block of trilithon.”
Since the above is hard to conceptualize, the author includes a drawing of the simple, yet effective solution to moving the trilithon.

Simple, workable, and human. Once again, the ancient alien theorist’s low view of human intelligence and practical engineering prowess is demonstrated.






b”h
The wiki article on Baalbek cites Jean-Pierre Adam’s work and says the quarry was higher than the construction site, meaning transporation of stones was “downhill” slightly.
http://en.wikipedia.org/wiki/Baalbek#Moving_the_stones
thanks!
thanks for the pictures! but reading the “translation” from the french was torture. you need a friend who speaks the language.
agreed; overly wooden and awkward.
Very good info and thanks for posting! I don’t know how the ancient alien/nephilim groups overlook this type of info. All they have to do is dig a little bit for many of their answers. Do they just not know where to look? I don’t want to think they are all dishonest, but it seems that way sometimes. Especially with this subject.
The people promoting the ideas that we need nephilim to explain megalithic architecture simply aren’t looking for real scholarship, or don’t know where to find it. I hate to be that blunt, but it’s that simple. Amateur researchers (and that’s not to be taken pejoratively — some amateur researchers are heroically tenacious) often equate knowing how to find books in a library and being able to read with academic research. That is a false equation. The books on a library shelf are starting points or summaries of someone’s work or thoughts. That is true even of academic libraries, though the stuff on the shelves is of much higher quality. The real scholarly discussion of practically anything is done in the academic journals, because THAT is where members of the guild talk TO EACH OTHER. Getting information from websites, magazines, and stuff sold in Barnes and Noble is surface analysis (or just plain junk). 90% of what scholars publish will never be sold in a Barnes and Noble. Things like graduate school take a person with the will to research and opens this other world to them.
This article is simply amazing; these were like the biggest stones ever in the time of augustus..
A wise friend explained to me not long ago, that angels were the original aliens, makes sense to me, after all they had God. Oh so do we by the way
not sure what the point is. Your friend doesn’t sound too wise, given the way angels are described in a range of ancient texts.
Interesting facts !
But there are more options.
For example the use of a canal.
See:
http://www.scribd.com/doc/103084449/CANAL-for-the-BAALBEK-STONES-transport
Kind regards
thanks for the link!
Link has been deleted Sept 2012
N
I’ll have a look and then find another one; thanks!
I just checked the links and they work – ?
For the deleted link of the canal, try another link:
http://www.scribd.com/doc/114544707/CANAL-TO-TRANSPORT-THE-BAALBEK-FOUNDATION-STONES
Very nice article. One tragic flaw in it. Ancient Alien theorists don’t care about monoliths moved during the last 3000 years. The “Ancient” refers to the fact that these monoliths (trilithon, the Easter Island monoliths and Stonehenge) are believed to be more than 3,000 years old making that technology unavailable.
That’s no flaw. If ancient people can do this without the wheel at one date, and the items used to do so existed at an earlier date, the only reason it may not have happened is that HUMANS didn’t think of it or have the need. There’s no need at all for aliens here, anywhere.
And of course there’s only one problem with that belief – there’s no data for it. But that never stops the AA crowd.
We don’t need to have aliens.
Why can’t you imagine that there MIGHT have been ancient civilizations from Earth that were more advanced.
There was a major flood, so we only have traces left.
You can’t deny some archaeological findings are out of place.
But you need the proof, you want to see the nuclear plant from 100.000 years ago or you won’t believe.
Some things are true even if not yet proven, and it’s people keeping an open mind that make great discoveries and are reminded by all centuries after.
Not people sticking to only one theory and unable to think out of the box.
I am not an AA person, I just accept the possibility that this theory might be true.
Your theory might be true too.
Don’t be sectarian…
And by the way, 3000 years ago would put us at 1000 BC – 1500 years AFTER the pyramid age, so, uh, the technology would have existed. Again, the AA crowd doesn’t care about such things.
Pyramids might be far older….
There are NO hieroglyphs or other markings inside allowing to date the beginning of the work on the Gizeh pyramid.
It is SCIENTIFICALLY proven that the Sphinx has water erosion marks dating from something like 10.000 BC.
Your theory is also just that, a theory.
The element of time is not taken into account by either party here. Many large things can be moved in 100 years or more. Some may have taken (hundreds) of years to build. Progressive projects could take even longer.
The pyrmids were made in less than 20 years…
That’s what mainstream archaeologist say based on false evidence…
We were not there, so we have currently no means to know for sure when and in what amount of time these pyramids were built.
Please refer us all to the studies demonstrating the falsehoods.
Don’t need a study for that.
Building pyramids in 20 years imply moving into place 1 block every 8 minutes, working day and night…
Common sense is a skill mainstream archaeologists seem to have lost.
They dicard everything that doesn’t suit their nice little theory.
There is not a single inscription in the Gizeh pyramid, no body was found inside.
If it was supposed to be a tomb for a great king, I guess hieroglyphs should be everywhere, statues, depictions of his greatness.
Furthermore, I don’t say for sure that my theory is the right one, but I accept the possibility that other explanations exist.
An open mind is the key to real understanding.
Ancient Aliens fans are like religious people; Once you accept the alien faith, it’s difficult to understand there’s a simpler way to explain those things.
We humans are intelligent!, no need of aliens to build pyramids and stuff.
Yeah ’cause it is ABSOLUTELY IMPOSSIBLE that other intelligent life exists anywhere else the universe or that that life could have made it here..
So, let’s examine the brilliant logic here. Because we *think* or *believe* life could exist elsewhere (we actually don’t know) then we can further *believe* or *speculate* that life came here, and then we can further *believe* and *speculate* that they built something.
Awesome. Really compelling thinking. Let’s not look at the fact that humans (which we know exist – !) could do this in the past (we have actual examples). Let’s go to speculating about beings we don’t know exist. Why not leprechauns instead?
Yeah ’cause it is ABSOLUTELY IMPOSSIBLE that other intelligent life exists anywhere else the universe or that that life could have made it here.. You do know the universe is REALLY OLD and REALLY BIG don’t you?
You really haven’t read much about me, have you? Over on my UFO Religions blog I say with complete clarity it doesn’t matter to me if there are ETs. It would be cool. But there’s just ZERO evidence for it.
I never said it was impossible ETs exist – you added that, and you don’t get to re-write my post.
Let’s try reading and thinking a little more clearly, since what you post here lives a really long time for others to see.
Why would you think these very intelligent being would leave any trace for dumb people?
But when you connect the dots from hints ALL OVER THE WORLD, you might begin to see that there is much more to reality than what you read in mainstream archeological textbooks.
It’s really sad you can’t have an open-minded view on this…
So, let me get this straight … you’re going to refer to “proof” of alien intervention, and then you ask us all why aliens would leave any proof for dumb people? There’s a disconnect there.
It’s not impossible that AA theory is the truth.
It’s not impossible that archaeologist are right.
If you can’t accept that, I guess I am out of this discussion 🙂
Blessings to all of you
There’s an unfinished piece still in the quarry. I suggest you validate your theory by moving it into place using the method you just described.
This is kind of a dumb reply. It’s like saying “hey, there’s some wood over there. I suggest you cook all your food over an open fire to prove to me that’s how it used to be done.” It literally has nothing to do with the topic. If ancients (and moderns without cranes) had methods for doing this sort of moving *then those methods existed* whether we still use them now or not.
You seem to forget that this is a theory. You are right, making a fire doesnt have anything to do with the subject because we all have made a fire and we have proof it is real. Why dont you just send us all a link of a person moving an 800 ton rock in this way?
You seem to be operating under the assumption that I presented it as the only option. I didn’t.
I suggest you think a little more carefully. If the stones that aren’t in the quarries b/c they were moved can be explained by applied physics, there is no reason to think that a monolith from the same location couldn’t be (AGAIN).
So……Ancient man sat on his ass all day while Aliens built everything ??
The picture above shows dirt all the way up to where the trilathon sit….the trilathon are 20ft in the air,are we to believe they buried it after construction then dug it out again? and that the ground was so compact you could put in a pulley system that carries 200T? And the picture above?? Oak around each end most definatly could not support that weight!!! I don’t think it was Aliens, I believe in a lost civilisation but these awnsers make less sense than aliens.
3000 seems a very conservative number, these blocks clearly predate the Romans and possibly the Egyptians, I am not convinced the Egyptians built all of the pyramids, or that these ruins are not even older than the pyramids. I think it is more likely that our ancients were capable of space travel than it is for an alien race to have visited. Although I am open to any and all theories. We must be open to all possibilities.
Nice article for a lot of different reasons! Although it still needs further testing from the perspective of someone or some engineer in 25 B.C. or earlier but at least it is a starting point. The nice thing about a theory is that it can be tested for validatity and data; from there it can be proven wrong or proven right; but worse case scenario it causes people to think of the possibilites. The “Ancient Astronaunt Theoriest” should not be ridiculed but thanked for forcing us to challenge our own limited beliefs. If you think about it what is wrong with an ancient civilization; either from here or up there; with technology far more advanced than our own; or our ancestors; who instructed earlier humans on how to build megolithic structures and other astounding things? If we are wedded to beliefs; be they religious or otherwise; we shortchange ourselves by limiting our capacity to think; we owe it to the human race (because there is only one race and that is human as far as we know) to remain open to the possibilities.
The consensus seems to be there are only two possibilities here, one, that some group of neolithic barbaric hunter-gatherers wound up some ropes and primitive pulleys to move the blocks….or Aliens did it. Both of which seem a little short sighted to me. The fact they were moved is self evident. But not the fact of how, why, when or by whom. As those parameters are unknowable at this time, everyone needs to chill a bit, and look at rational (testable) explanations, then test and re-test those parameters until a reasonable hypothesis can be developed. All the rest is buffoonery. Talk about the woo-woo crowd…..
Here are some alternatives to both positions…
1. One or more previous technically advanced cultures might or could have had monolithic moving technology that was used to move the monoliths. Those technologies might or could include attenuation of gravity or other electrostatic variance, electromagnetic ‘density’, acoustic or any of dozens of other ‘wave’ technology manipulations (which will create a limited ‘anti-gravity’ environment).
2. One or more previous technically advanced cultures might or could have had several ‘hominid’ (or more correctly ‘hominin’) species, one of which were ‘giants’ of a size larger than the historical record of the giants of Bashaan. (About 12′ 5″ tall). As giants are part of our historical and archaeological records, it seems like a reasonable place to start a dialogue for a hypothesis.
3. One of more previous technically advanced cultures might or could have had flight knowledge, technologies and capabilities, (although NOT from external or ‘extra-terrestrial’ sources, but from local or ‘original terrestrial’ sources) moving the stones with that capability.
4. Or, as the current situation demonstrates, we have absolutely no clue. Which should not be an excuse for buffoonery.
5. I, or you can ‘like’ any of a dozen possible or even rational explanations, but what we aught not to do is argue for or against any of them until they have been rigorously tested. Advocates and de-bunker alike should adhere to this basic principle.
Finally a clever alternative 🙂
Did you by any chance notice that the Thunder Stone, was moved on ice??
They had to wait for the ground to be frozen…
Unlikely to be possible in the uneven rocky terrain in Lebanon.
You compare apple and pears to validate your theory of pseudo-scientifico-babble.
Furthermore, old heavy stones were dated more 10.000 years old, before the technology you refer to was even supposedly available…
no, they weren’t dated to that age – but please give us all the link to that study.
the site of yonaguni is underwater, so at least 10,000 years old.
I guess you will as me for a study proving that it is not a natural formation 🙂
you’re right – I’d like a study so I can post it. But this is beside the point. Let’s assume it’s ten thousand years old. On what basis does that inform us about a structure on thousands of miles away representative of a different culture? So it’s 10K years old – I’m saying it’s still entirely human technology. So let’s see the evidence for non-human technology.
Point: Are you arguing for alien intervention? First you need to establish there are aliens, else you assume what you need to prove:
– there’s a really huge old structure located at X.
– I can’t think of a way humans could have built it.
– aliens must have built it or helped.
– therefore, there are aliens.
– and so we’ve proven aliens built X.
It’s circular. But if the point isn’t aliens, I’m not sure what you’re pressing for.
I’m not pressing for AA.
I just think more advanced HUMAN civilizations (socially, ethically, mentally AND technologically (non-invasive, polluting, technology), far more ancient than mainstream archaeologists think, might have existed before the flood, and disappeared leaving almost no trace because of the tragic and catastrophic events (the flood) that occurred on our planet.
But I do not discard aliens. I just do not know. We have no solid evidence, it does not mean we won’t find any one day. But you’re right, aliens are not needed to explain very ancient structures.
Still, these structures ARE there, lime Puma Punku, and if there were no aliens involved, humans must have had an advanced way of cutting and piercing the stones.
Obvious.
You keep referring to the “flood’ as the demise of an ancient civilization that may or may not have existed as the culprits that may or may not have built all these ancient ruins…. Are you :Bible Thumping”?
Religion is belief in someone else’s experience.
Spirituality is having your own experience.
These discussions are pointless and don’t make any sense.
You don’t know the truth more than I do.
Meditate, turn your attention inwards, that’s all that is needed.
I’m out of this conversation.
Blessings to all
I guess you are without proof for any of this. This is an evidence-driven blog.
Did you ever try to meditate and get intuitive information from inside without needing a proof coming out of reasoning, from outside?
Basically that’s what Jesus and all spiritual teachers told us to do:
“The Kingdom of Heaven is inside of you” ==> MEDITATE, SHOW LOVE, RESPECT OTHERS.
Have fun arguing on wether Sitchin is right or wrong, or how did they move these stones while the planet is being destroyed by our unhealthy habits.
Then you will tell me this is out of subject.
You can reply whatever you want, this is my last reply on this blog.
Only the inside subjective experiences are real and tell you the truth, not unproductive continuous argumenting on the Net to prove your theory is right and someone else’s theory is wrong.
Time to grow up a little bit a focus on what’s truly important: THE PRESENT.
Happy new year 🙂
The musings of my head and heart don’t inform me about ancient construction techniques. Neither do yours. Just doing something else Jesus said to do: tell the truth.
Ok, I will post one more thing.
To understand how these advanced people moved these stones you mlght want to watch some videos on the work of Nassim Haramein (physicist, scientist) (it will take you 10h tough).
After that, we can continue this discussion.
What he says will maybe give you a new understanding of reality.
https://vimeo.com/78989902 (just as a teaser)
https://www.youtube.com/watch?v=TkbNjGC6An8
resonance.is official website for a new kind of physics (the one ancient civs were using)
If you decide not to watch, then we can’t of course DisQus it 🙂
You are right, Jesus said to tell THE truth, not YOUR truth.
Love each other and do good to others as if it were yourself.
Apparently you have a hard time standing points of vues different from yours.
Maybe you should sometimes consider NOT HAVING THE LAST WORD :).
Ego is a dangerous thing.
Happy new year.
The techniques are valid with or without ice conditions. Other methods (e.g., gravel) are known that assist movement if needed. I suppose your alternative is levitation? Lots of real world examples for that.
It took the British Admiralty over forty years to convince the scientific community then, that Scurvy could be cured by eating oranges.
They thought that was too fkn simple too.
You would have greatly benefited from reading the last scientific studies on the quarries and the two trilithon stones still in place published by Dr Jeanine Abdul-Massih, who has been studying them within the Project “Urban Development in Baalbek” between 2003-2012. Look up BAAL Hors Serie IV as a starter.
A – Life abunds in the universe.
B – Life in any planets, are implemented artifically. All planets are terraformed, life artificially developed in order to create a vessel where consciouness can inhabit.
C – As in all other planets, such as the EARTH, civilizations came, tought some STUFF, to its people, and did what the have to do. genetical manipulation. We live in an open lab, where reports to abduction and sexual intercourse with beings human or close to human happen all the time.
D – They hide partially the evidence, but they leak enought to connect the dots as a friend told above. We seriously are suffering from cognitive dissonance. If you read any ancient text, I said any, you will find the same sort of pattern, technological beings dealing with primitive beings. At some point there is some marriage or rape, and the like. Also a lot of teachings, and fitghting with the neghbours who are defined as inferior.
It is easy to come here, and throw to us, a lot of “established facts” made out by i”ntelectuals” from the XIX highly charged with ideology and authority, and make us swallow this buch of “rational” unproven, and unscientific data.
I am sorry, BUT IT WONT STICK OK?
I will tell you something, you religious guys up there, that quote the Bible, to say it is the work of G-D. I tell you something. Torah Emet. That means, the truth above all. These beings may be teaching about the Creator of all. But following the same rationale, of the thinkers, who were defining what G-D actually is. You may take the Rambam, or the Kabbalah if you will, what we see, does not follow their definition, is a contradictions.
SO WHAT ARE THEY?
HOPE I WAS VERY CLEAR GUYS, IF YOU WANT EASY ANSWERS, GO BUY SOME FASTFOOD, AND DREAM ON, BUT IF YOU WANT REAL ANSWERS, ONLY THE REAL RESEARCH WILL DO OK?
I will not even bother in putting up a bibliography, the Baalbec site is clear much older than roman times, it hasn´t any characteristic of the roman constructions, so it is idle to discuss here with closed mind people, for those who want real answers, jus let this people talk among their peers. It is a battle of information and ideology I am afraid, and perhaps there is lot at stake, but perhaps it is just one more of the puzzles these people, those BEINGS left us with up to know.
It is the same pattern of the Crop circles, hide and seek, show and then hide again. For the ones who believe in their capacity of believing in its own perception, will may get something, but if you wait to people feed you with truth, as I said above, just sit and wait, forever.
Real research? Like what you offered for your first point? What evidence do you have that NASA and SETI don’t for the claim that the universe teems with life. In real-ville, we just don’t know that factually — that’s why scientists are still looking for it. Thanks for that real research.
Your other ideas extend from this unproven one, so we don’t get real research there, either. Like — do you have evidence anyone is hiding evidence? (Have to love the circularity there). Conspiracy theories aren’t, by definition, evidence. They are, well, THEORIES.
What a dead end.
Haha, left brain scientist will never find any truth.
Mister Heiser, if you genuinely think all crop circles were made by Jack and Joe using snow shoes,
it is really pointless to discuss.
Mainstream science is based on division, not unity.
It does NOT include consciousness (which is not generated by the brain but we are the consciousness of the multiverse, please meditate to find out)
Advanced civs WERE there, it is SO obvious that they had technology to lift the stones.
Where is this tech then?
The Ark of the Covenant would suit your needs, I guess.
A device that can split the Red Sea in 2 is enough proof for me.
To know where is the Ark is now, please watch the video from Graham Hancock.
Wake up mate, accept YOU’RE WRONG 🙂
You feel better after; you’ll see.
I did it many times, I have no problem with admitting my mistakes.
But it’s not the case here.
To understand the physics of the ARK watch the video of Nassim Haramein (Rogue Valley 2003) on YouTube
Wish you a good awakening.
Your comments make little sense. You seem to look for things to assume about me that I never said (like the circles). And any side of the brain, devoid of data, resolves nothing. Let’s hear an example of how a data-less right brain solved anything – remember, no facts please.
Haha, I’m done here.
You will never understand.
THERE ARE NO ALIENS, ALL THE UNIVERSE IS INSIDE EACH OF US.
It’s only a more evolved part of OUR consciousness that people call aliens.
Please watch the videeos from Haramein (I sent the link).
Read the Gospel of Thomas and the Pistis Sophia and the Book of Jeu
(I’m sure you have) with a new eye.
Read the books of Giuliana Conforto.
The universe also is going in circles (or in a vortex motion), not only me.
If you spend your entire life looking for proofs or facts in the material world, then I’m very sad for you, because you won’t find any.
http://altering-perspectives.com/2013/06/giant-pyramids-and-sphinxes-found-in.html?utm_source=tipw
All of the mechanical motion drawings are decidedly convenient. For me, the great elephant in the room (never addressed) is the absent narratives for:
a) separating stones that large from the underside physical bond with the ground.
b) the mechanics for how the stone was initially lifted into the contraption of choice.
c) the reason for why any cellulose contraption would not compress like a sponge into a locked state under such weight.
The NULL hypothesis says: normal humans cannot do a and b and c for stones that large.
Please falsify the NULL for me.
Everything you mention here is actually addressed in scholarly books and articles that aren’t accessible online. All you need is applied physics that is scalable. I can give you titles, but you’d have to buy the books and find a library that will give you access to PDFs (depending on what it is, I might have an article you’d want – but my own collection is far from complete). But there’s a PILE of scholarly literature on ancient architecture. It’s not a small field.
But even though those models exist (again, for every point you raise), such models are still hypothetical. We don’t know (for the most part) what methods they used. It’s only know how they COULD have done it, based on classical source texts, drawings, even diagrams on the blocks (like at Baalbek).